Интерференция наблюдается в результате сложения двух и более волн, частоты которых совпадают. Если в такой картине возникают не изменяющиеся со временем чередования максимумов и минимумов, то мы говорим о стоячей волне. Она возникает благодаря тому, что налагающиеся волны имеют одинаковый период и неизменный сдвиг фаз колебаний в каждой точке (когерентные волны).  Устойчивая интерференция может иметь место только при условии когерентности волн, и это самое главное условие получение волновой интерференционной картины. В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения.

На рис.2 показаны разные картины интерференции двух волн в зависимости от частоты колебания и расстояний между центрами колебаний. Темные места в этих картинах связаны с точками, где происходит гашение колебаний, а светлые – с усилением амплитуды за счет сложения колебаний. Гашение колебаний в одних местах и усиление в других при интерференции волн не связаны с какими-либо превращениями энергии колебаний. В точках, где колебания от двух волн гасят друг друга, энергия волн не превращается в другие виды, например в теплоту. Все сводится лишь к перераспределению потока энергии в пространстве, так что минимумы энергии колебаний в одних местах компенсируются максимумами в других в полном соответствии с законом сохранения энергии.

Наблюдение интерференции от двух волн, как на рис.2, является самым простым случаем сложения колебаний. Куда более сложные и красивые интерференционные картины получаются при сложении трех и более колебаний. Наглядный и красивый способ наблюдения стоячих волн в пластинках придумал в 1787 г. немецкий физик Эрнст Хладни (1756-1827). На пластинку из стекла, металла или дерева, закрепленную в нескольких точках, насыпается песок. Стоячие волны в пластинке возбуждаются тем, что по ее краю проводят натертым канифолью смычком. Песок сбрасывается с тех мест, где происходит усиление амплитуды и собирается на узловых линиях, образуя так называемые фигуры Хладни.

Эти фигуры показывают картину узловых линий, рассекающих поверхность пластинки при ее колебаниях. Вид фигур зависит от формы пластинки и положения закрепленных точек, а также от того, в каком месте проводить смычком.

Рис.2. Интерференции двух волн в зависимости от частоты колебания и расстояний между центрами колебаний. Темные места образуются за счет гашения колебаний, а светлые связаны с усилением амплитуды в результате сложения волн.

Несколько позже доктор Ханс Йенни усовершенствовал эксперимент Хладни. Он наблюдал интерференцию не только на плоскости, но и в объемном варианте. Для проведения своих экспериментов Йенни создал специальный аппарат, который назвал тоноскоп. Он получал геометрию звуковых колебаний, используя тонкие контейнеры, наполненных различными средами: песком, мокрым гипсом и разными типами жидкостей, состоящих из тонкодисперсных сред. Находясь в состоянии покоя, взвесь мельчайших частиц равномерно распределялась по всему объему жидкости, и вода становилась мутной. Когда контейнер приводили в колебательное движение с различной частотой и амплитудой, частицы в жидкости складывались в упорядоченные и хорошо видимые геометрические узоры, обладающие двумерной и трехмерной структурой (рис.3А). На рис.3Б представлена интерференция волн, которую Йенни получал в вибрирующей капельке воды, содержащей мелкие частицы взвеси. Эти частицы формировали трёхмерные звезды, двойные четырёхгранники в кругах и много других фигур. Чем выше была частота колебаний, тем сложнее получались фигуры.

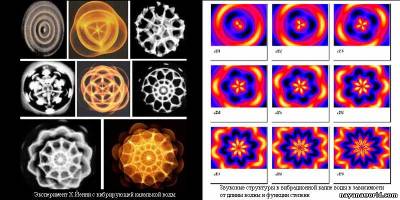Рис.3. Фигуры Хладни.

Современные исследователи явления интерференции еще более усложнили эксперименты. Вместо крупных твердых частиц теперь используются всевозможные взвеси тонкодисперсных веществ, струйки пара или дыма и др. И всегда получались изумительные узоры, представляющие собой картину интерференционных полей (см. рис.4).

Посмотрим, каким образом получаются такие красивые интерференционные картины. Как уже говорилось, явление интерференции наблюдается при сложении когерентных (одинаковых) волн. Источником колебаний являются звуковые волны. В нашем случае, будь это пластина или капелька воды, пространство является замкнутым. Поэтому волны, участвующие в интерференции, образуются за счет волны, распространяющейся от источника колебания, и волн, отраженных от границы пространства. Построение правильных геометрических узоров зависит от частоты колебаний и размеров пространства, только  в том случае, когда в пространстве укладывает целое число полуволн, мы наблюдаем явление интерференции.

Колебания на пластине или внутри пространства создают волны, которые, интерферируя между собой, создают устойчивые волновые картины. Глядя на получающиеся картины, мы видим, что частицы скапливаются в тех местах, где отсутствует какая-либо вибрация. Такие области образуются за счет гашения колебаний и соответствуют минимальным значениям энергии. И наоборот, области пространства, в которых происходит усиление амплитуды в результате сложения колебаний, свободны от частиц. Их само пространство как бы выталкивает из этих мест. Поэтому, благодаря мельчайшим частицам, мы можем наблюдать сложную картину интерференции, создаваемую колебательными процессами.

Таким образом, получаем, что интерференционные минимумы, где скапливаются мелкие частицы, являются энергетически более выгодными. Поэтому частицы стремятся занять область с минимальной потенциальной энергией. В местах интерференционных максимумов появляются как бы потенциальные барьеры, которые не позволяют частицам свободно перемещаться в пространстве. При отсутствии колебаний мелкие частицы могли свободно диффундировать по всему пространству, равномерно заполняя весь объем. Но интерференционные максимумы создают «непреодолимый» барьер для диффундирующих частиц, поэтому они скапливаются только в местах интерференционных минимумов.

 Рис.4. Энергетическая структура сложных интерференционных полей

Еще раз хочу обратить внимание на то, что гашение колебаний в одних местах и усиление в других при интерференции волн не связаны с какими-либо превращениями энергии колебаний. В точках, где колебания от двух волн гасят друг друга, энергия волн не превращается в другие виды. Все сводится лишь к перераспределению потока энергии в пространстве, так что минимумы энергии колебаний в одних местах компенсируются максимумами в других в соответствии с законом сохранения энергии.

Интерференционная картина, получающаяся благодаря мельчайшим частицам, таким образом, отображает энергетическую структуру пространства или среды. Поэтому, когда в среде возникают вибрационные процессы, то вместе с этим в ней возникает и пространственная структура, т.е. появляются области с разной потенциальной энергией. Эта структура оказывает существенное влияние на распределение посторонних частиц внутри среды.

Теперь представьте, что в такой вибрационной среде будут распространяться посторонние частицы или волны. Естественно, что энергетическая структура такого пространства будет оказывать существенное влияние и на их движение. До сих пор мы рассматривали, какое влияние оказывает вибрационная среда на неподвижные или диффундирующие частицы. При этом видели, что светлые места, или места скопления частиц, соответствуют потенциальным минимумам. А темные места являются потенциальными максимумами, в которых частицы не могут находиться в спокойном состоянии. Поэтому в «светлых» местах (линии узлов) движущаяся частица будет проходить без потери энергии. В то время как по темным участкам интерференционной картины частица будет тормозиться и смещаться в сторону потенциальных минимумов, т.е. места интерференционных максимумов создают для нее «препятствия», что-то вроде трения. В этом случае линии узлов можно рассматривать как волноводы, по которым частица распространяется без потери энергии. А темные участки представляют собой потенциальные барьеры, препятствующие прохождению частиц. Аналогичная картина будет наблюдаться в такой вибрационной среде и при прохождении волн. По волноводам (линии узлов) волна проходит без потери энергии, а проходя по энергетическим максимумам, волна будет терять энергию.

Таким образом, мы видим, что интерференция сама по себе достаточно интересное явление. Но особое значение представляет собой появление в пространстве энергетической структуры за счет внутренних полей вибрации. Потому что эта структура способна оказывать влияние на все объекты, находящиеся или перемещающиеся внутри ее пространства. Теперь, зная свойства интерференционных полей, мы можем рассмотреть, как образуется реальность мира в виде голограммы, какую роль в ней играют структура пространства и материи.